Gravitation
Orbital mechanics describes the movement mass bodies in a vacuum and subject only to the laws of gravitation.
Gravitation is an interaction that creates a force of attraction between two objects with a mass. The value of this force is given by the formula:
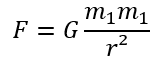
F: the gravitational force exerted by the two bodies expressed in N
G: The gravitational constant always equal to 6.6742-10-11 N-m2-kg-2
m1 and m2: the masses of the two objects between which the interaction is created , expressed in kg
r. radius, the distance between the centre of gravity, expressed in metres
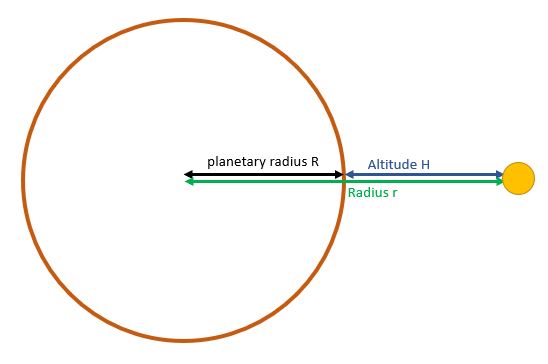
distance in orbit
The radius simply refers to the distance between the center of gravity of the two bodies. It differs from the altitude h that separates the satellite from the surface of a planet. To pass from one to the other, it is necessary to add the radius of the planet R or more often Rx (with x the first letter of the name of the planet to avoid confusion), that is to say the distance between the center of gravity and the surface.
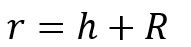
This force is reciprocal, that is, attracts the two objects to each other with the same force. So the Earth attracts you with as same force as you attract it. As the mass of the earth is far greater than yours, the force you apply to it has a negligible effect on its behavior.
However, the Gravitational attraction of the Earth on you is the main force that governs your movements. This preponderance is such that the attraction of another object close to you (vehicle, building, person) is negligible compared to the strength of the Earth.
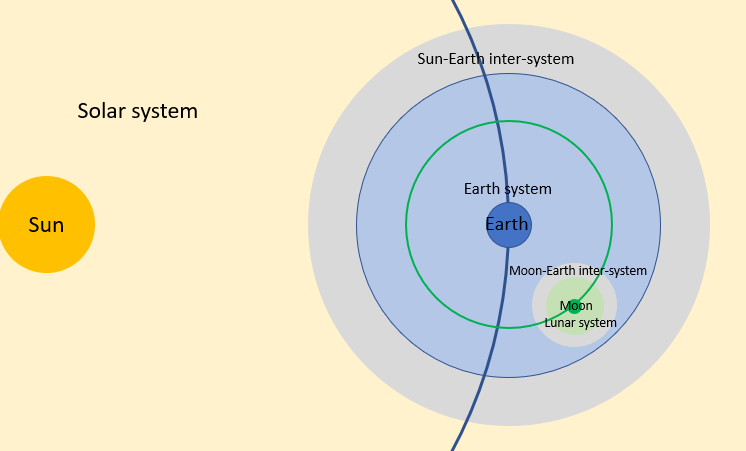
System
This preponderance of one object over the others creates a notion of a system. A system is a volume restricted around a massive object (dominant object) or each point is much closer to the dominant object than any other object of equal or greater mass. The other objects of the system (dominated object) therefore have a much lower mass. The dominant force on the dominated is the only taken into account. The forces of the dominated over the dominant, the dominated among themselves and objects outside the system on the dominated is neglected.
Systems can be intertwined. For example, the solar system sun dominate the planets, but each planet has its own system. In the Earth’s system (where the Earth is the dominant object) the trajectory of the satellites is governed by the Earth, and not the sun, more massive but more distant (the force of attraction depends on the square of the distance).
The notion of system is imperfect because, by moving closer to the borders of a system, dominated objects (such as terrestrial satellites) are increasingly disrupted dominant objects of higher (sun) or lower (moon) systems, to the point where permanent corrections are needed. You can even place an object between two systems and have a trajectory governed by both dominant bodies (example NRHO orbit).
To simplify the calculations within a system, the standard gravitational parameter of the dominant body is introduced, which is simply calculated by:
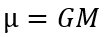
With G the gravitational constant defined above and M the mass of the dominant body. In the international unit system (metric) it is expressed in m3 /s², but for practical reasons, in orbital mechanics it is often the km that is used for distances. It is therefore often expressed inkm3/s² for a factor of10-9 on the value in m3 s-2
trajectory and transition velocity
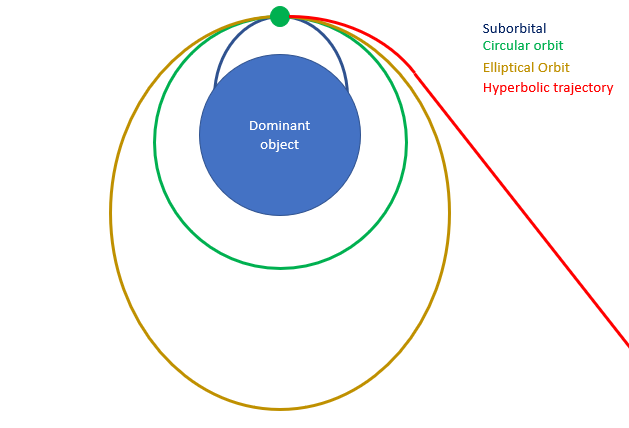
A body dominated that moves in a system possesses an energy that, for lack of friction, does not vary. This energy is divided between kinetic energy which depends on the velocity and potential energy that depends on the radius. A body dominates converts part of its velocity into distance or distance into velocity. Depending on the energy level, it can follow 4 types of trajectory.
Suborbital (v <v1): If the velocity is too low, the centrifugal effect is not enough to compensate for gravity. The body descends to regain velocity. If it descends too much, the radius becomes smaller than the radius of the planet and is crushed. it is impossible to keep it in space. Since the object is unable to make a full orbit, this trajectory is called suborbital.
Circular orbit (v = v1): If the body has just enough velocity for the centrifugal effect to compensate for gravity. The body always stays at the same velocity and altitude. It makes circles around the dominant body hence the name circular orbit.
Elliptical orbit (v1 <v <v2): If the velocity is important enough for the centrifugal effect to exceed the gravitational pull. The dominated moves away from the dominant by converting his velocity into a radius. After a while, the velocity decreased too much to compensate for gravity. the object therefore begins to descend and resume velocity. The dominate ends up passing the initial point at the same velocity and went back up in a cycle of perpetual descent. It follows an elliptical circuit which gives it its name of elliptical orbit.
Hyperbolic trajectory (v2 <v): If the velocity is really too high, the body moves away to the point where the gravitational force becomes weak. The velocity decreases less and less as the body continues to move away. Finally, he walks away forever and does not return to the dominant body.
For determine where you are, you have to calculate the transition velocity:
The v1 orbiting velocity is the velocity required to reach a circular orbit.
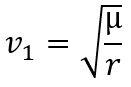
The escape velocity v2 is the velocity of passage from an elliptical orbit to an hyperbolic trajectory.
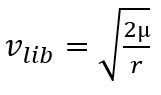
Non-energy setting
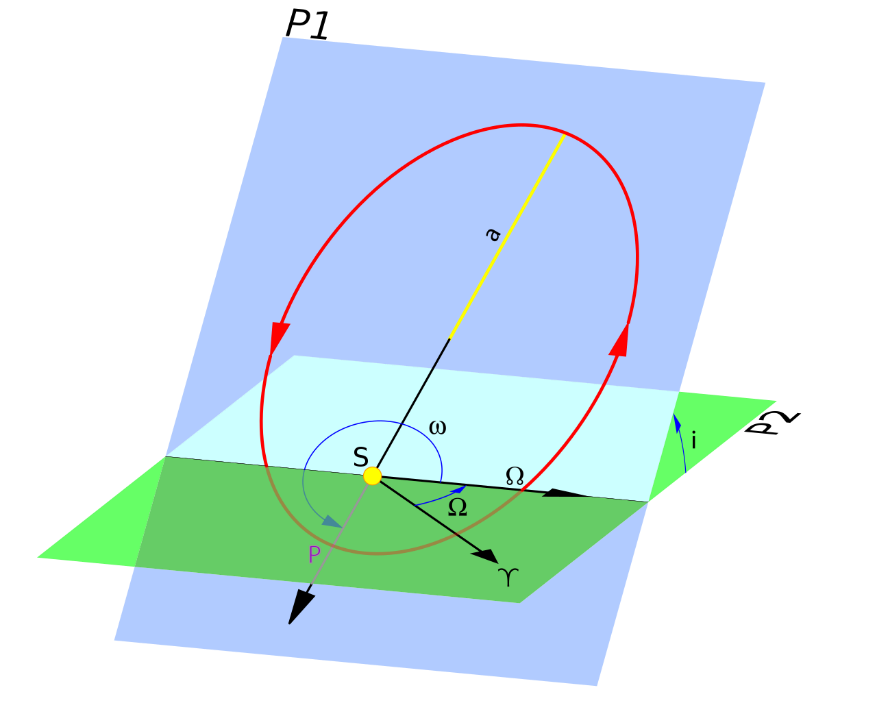
With the exception of specific cases, such as the orbits around the Lagrange points (example of the NHRO orbit) all The orbits are flat. The orbital inclination i is defined as the angle separating the orbital plane and a reference plane, which is the equator for a planetary system or the ecliptic (Earth’s orbital plane) for the solar system. if we take the example of the Earth, the inclination is at 0 when the satellite is in orbit around the equator in the prograde direction, i.e. from west to east, or in the direct direction (reverses hands of a watch) seen from the north pole. At 90 degrees tilt the orbit passes over the poles. At 180 degrees the orbit is equatorial but retrograde (reverse prograde).
The last thing to know is the periastre argument , which defines the angle on the equator between the reference point (called the vernal point) and the projection on the equator of the periastre.