A. Geometric settings
An ellipse is a closed conical, defined by a number of geometric parameters that have few physical realities, but which allows the calculation of the data of the orbit.
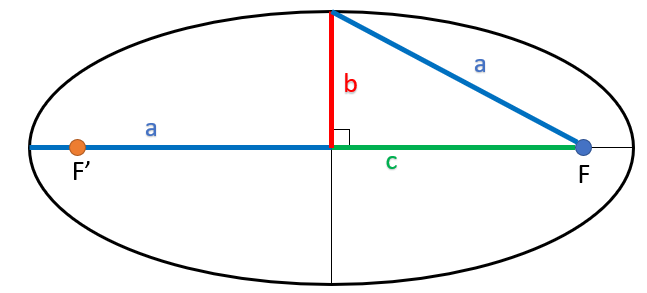
The focus F and F’ of which one (F) is the position of the dominant body.
The major axis 2a is the most large segment between two points of the ellipse, it passes through the F and F’ points. At each point of the ellipse (noted m) the sum distances Fm+F’m is equal to 2a. The value that characterizes the semi-major axis a is often used.
Linear eccentricity c which is equal to half the FF’ distance.
Eccentricity e is dimensionless parameter that describes the overall shape of the ellipse. If it is equal to 0, the two focuses are common with the center and the ellipse becomes a circle. If it is greater than or equal to 1, the ellipse becomes open (parabola or hyperbole) and from an orbital point of view one moves to a hyperbolic trajectory.
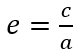
The linear eccentricity c dependent on e and a. so we can define an orbit with just a and e. a defined the size and e the shape of the orbit.
B. Observable Settings
Apart from these purely geomatic data, velocity and radius are observable data that allow to calculate geometric data and vice versa. Since we are looking for 2 geomatic data (a and e) we need a couple of two observable data located at the periastre or apoastre.
The perastre (perigee in Earth system and perihelion in solar system) is the point of the orbit closest to the dominant body.
The apoastre (apogee in the Earth system and aphelia in solar system) is the point of the orbit furthest from the dominant body.
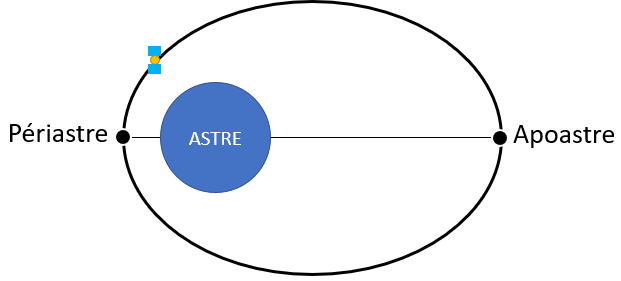
the radius at these points are often used for calculations and are noted Ra to the apoastre and rp to the periastre.
C. Calculations
data of radius at extremities
The first couple of data is the radius of the extremities that requires knowing the Rp and Ra. It simply means observing the moment when the dominated body passes as close and far as possible from the dominant body. Since the periastre and the apoastre are the furthest points from the orbit, it is easy to know a and e deduce the gap between the two radius.
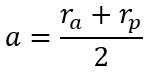
ra and rp: radius to the apoastre and the perastre
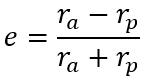
ra and rp: radius to the apoastre and the perastre
Conversely, on the use of the geomatic relationships of the extremities of the orbit and the focal point to know the radius from geomatic data.
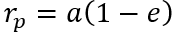
a : semi-major axis
e: eccentricity
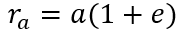
a: semi major axis
e: eccentricity
radius-velocity formula
If we know a radius at one point and the velocity at this point (the maneuvers are often done at the extremity, we know the velocity) we can also calculate the geometric data. For this we need the relationship between radius and velocity at any point of the elliptical orbit.
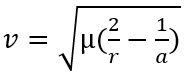
mu:standard gravitational parameter
r: radius
a: semi-major axis
By reversing it, we can calculate a at any point if we know the radius and velocity at this point.
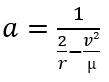
mu: standard gravitational parameter
r: radius
a: semi-major axis
couple of data at the perastre
So we can use the couple of data at the periastre, velocity and radius. We use the velocity<=> radius relationship to calculate a and e .
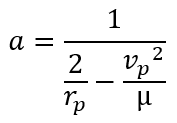
rp: periastre radius
vp: velocity to periastre
mu: standard gravitational parameter
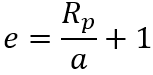
rp=periastre radius
a:semi-major axis
In the opposite direction with the geometric data, one can calculate the radius at the perastre with the velocity at this point with a dedicated relationship.
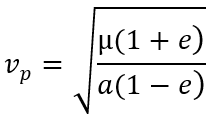
Data couple at apoastre
Similarly, the apoastre’s data couple can be used, including the radius and velocity and adapt relationships to find geometric data.
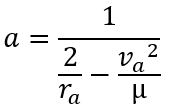
ra: radius to the apoastre
va: velocity to the apoastre
mu: standard gravitational parameter
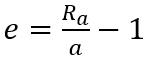
ra: radius a l’apoastre
a: semi-major axis
And in the sense of geomatic parameters to apoastre, we already have the radius, and the velocity is calculated as well.
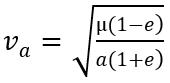
mu: standard gravitational paramet
e: eccentricity
a: semi-major large axis
D. circular orbit
The circular orbit is a special case of the elliptical orbit, its eccentricity is equal to 0. There is therefore no apoastre or periastre because all the points of the orbit are at the same distance r (r=a) of the dominant body. So we just have a relationship between radius and velocity.
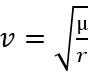
r:radius
mu: standard gravitational parameter
It is thanks to the circular orbit that the minimum orbital velocity is defined. Effect the minimum velocity for orbiting a planet is the circular orbit whose radius is just above the surface or its atmosphere if it has one.
E. Period
The period, that is, the time it takes the body to travel through its entire orbit, is calculated using the geometric data with the formula below and gives a result in seconds.
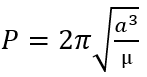
a: semi-major axis
mu: standard gravitational parameter
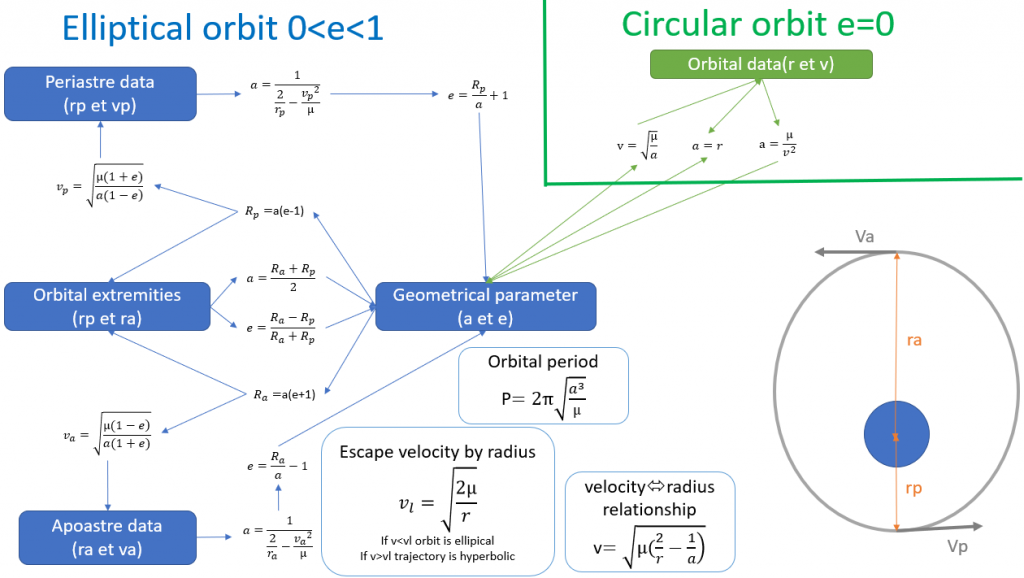
below is a summary of the formulas for past from one couple of data to another.
In order to make everything is more concrete calculation and better understand their usefulness, here is a digital application