A. Conjunction period
In addition to the calculation of autonomy, it is important to know the interplanetary shooting schedule. To do this, we study the movement of one planet from another (often the Earth). A dominated body away from its dominant body moves more slowly than a closer body. One can know the average angular velocity, omega, the angle in degree traveled per day from the formula of the period.
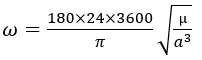
mu: standarda gravitational parameter
a: semi-major axis
Two planets that have by definition cleaned their orbit (they do not intersect) their semi-major axis is necessarily different, which implies a difference in angular velocity. The planets then engage in a chase game where the lowest planet catches up with the highest planet, passes between the planet and the sun and then overtakes it and continues until it returns in the other direction.
The conjunction theme is a term derived from astronomy that refers to the fact that two celestial objects are close seen from a third (Earth). There are two types, the lower conjunction when a planet (Venus or Mercury) passes between the Earth and the sun and the upper conjunction when a planet (any one) passes behind the sun. Here, by default the term conjunction refers to a lower conjunction and is used when the low planet passes between the high planet and the sun, this is the time when the two planets are closest and by default the measurement of the distance between the planets. When the sun is between the two planets (upper conjunction) we will speak more of opposition.
Since the planets do not have the same orbital inclination, during most conjunctions, the low planet passes above or below the sun seen from the high planet. Alignment is therefore a special case of a conjunction, which happens close enough to a node (coincidence of orbital planes) that the planets and the sun are perfectly aligned so that the low planet partially masks the solar disk seen from the high planet.
The synodic period, rather called the conjunction period, refers to the time that separates two conjunctions, is the time it takes the low planet to make one more turn than the high planet. It is calculated thus (expressed in days) with the average angular velocity of the two planet.
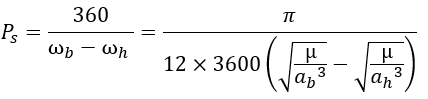
omega b and omega h: angular velocity of low and high planete
mu: standarda gravitational paramete of dominant body (Sun for planet)
ab and ah: semi-major axis of low and high planets
B. Shooting window
This period allows for an orbital calendar that determines the firing windows. A shooting window is a period during which it is possible to launch a ship from one planet to another. This window is defined according to the Dv needed to move from one planet to another, which reaches a minimum at the level of Hohmann’s trajectory and then believes on both sides. The firing window is the entire period when the Dv available to the spaceship is greater than the necessary Dv. It is getting weaker as the ship’s DV decreases, it becomes punctual (the ship must leave at a specific moment or wait for the next window) if the Dv available and equal to the minimum Dv (the DV of an interplanetary transfer from Hohmann) and the interplanetary path is impossible if the available dv is less than the minimum DV.
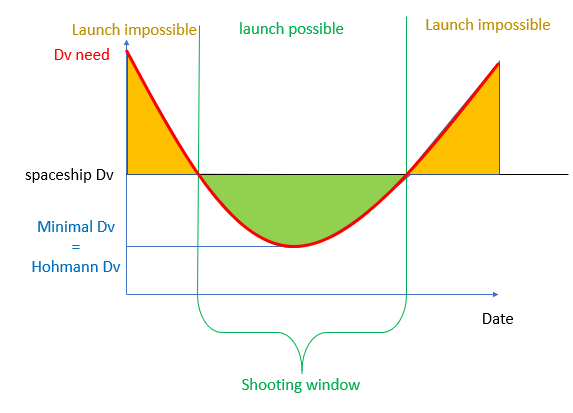
Since the window is centered on Hohmann’s interplanetary transfer orbit, it is necessary to determine when to print this orbit. We will start by studying the path of the high planet to the low planet. It is known by definition that at the time of the ship’s departure, it is at the aphelia of its transfer orbit. It will meet the low planet at the time of its perihelion. Given their semi-major axis, we know that in terms of angular velocity, the low planet will be the fastest, then the ship and finally the high planet will be the slowest. One must define the angular date – which is the angle that forms the high planet-sun axis with the low planet-sun axis, so it is zero at the conjunction, negative when the low planet lies behind the high and positive planet in the opposite case. This angular date can be converted to the date of conjunction D which is the number of days before (negative value) or after (positive value) the nearest conjunction.
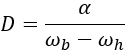
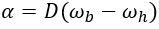
alpha: angular date
omege: average angular velocity
At the time of departure, the low planet must so be behind the ship and thus the high planet (angular date negative). At the time of arrival, the ship and the low planet are at the same and in front of the high planet that has been overtaken. A shooting window is therefore just before the conjunction, with an arrival after this conjunction.
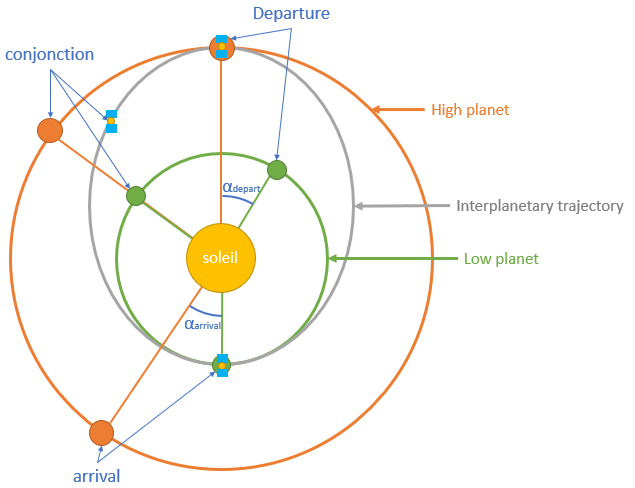
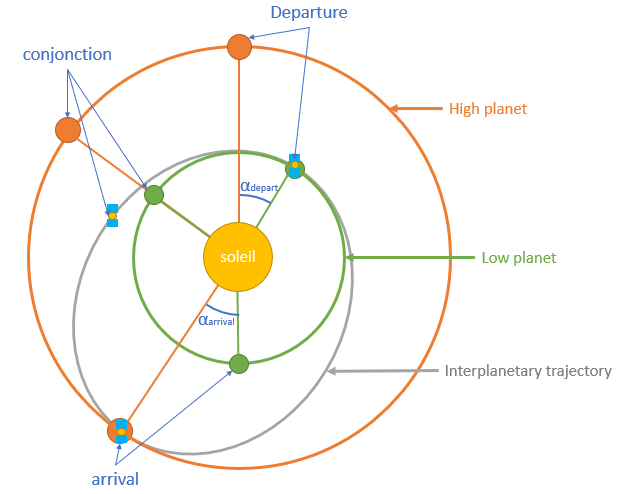
The situation is similar when made a trip from the low planet to the high planet. We even know that the time of departure and arrival in Hohman orbit for a low planet high planet journey and are the same for a low planet high planet ride.
The angular start and arrival date can be calculated either by knowing the angular velocity (in °/days) of the planets as well as the P period (in days) of Hohmann’s orbit or directly by knowing the semi-major axis ab and ahof the high and low planets.
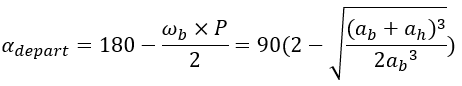
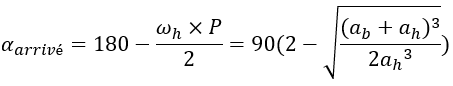
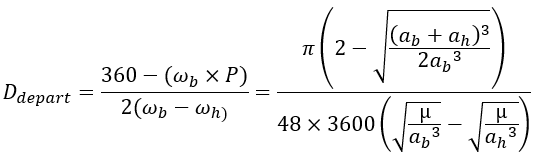
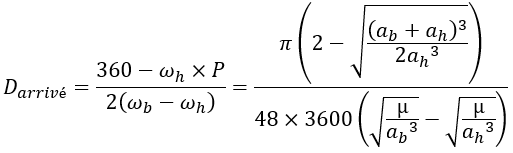
In order to make everything is more concrete calculation and better understand their usefulness, here is a digital application