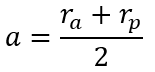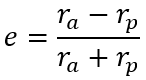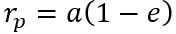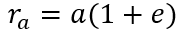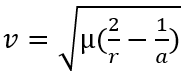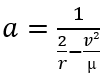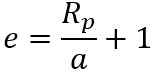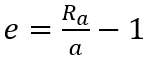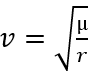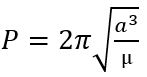A. Paramètres géométriques
Une ellipse est un conique fermé, défini par un certain nombre de paramètres géométriques qui ont peu de réalités physiques, mais qui permet de calculer les données de l’orbite.
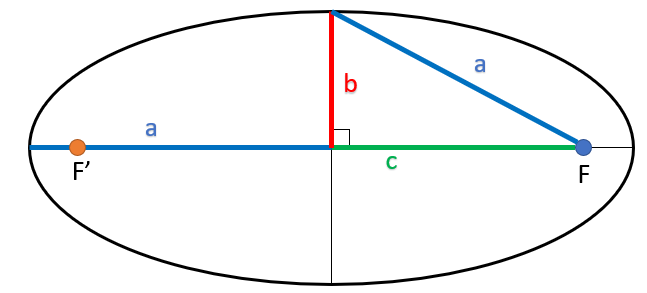
Les foyers F et F’ dont un (le point F) est la position du corps dominant .
Le grand axe 2a est le plus grand segment entre deux points de l’ellipse, il passe par les points F et F’. En chaque point de l’ellipse (noté m) la somme des distances Fm+F’m est égale 2a. La valeur a qui caractérise le demi-grand axe est souvent utilisée.
L’excentricité linéaire c qui est égale à la moitié de la distance FF’.
L’excentricité e est un paramètre sans dimension qui décrit la forme globale de l’ellipse. Si elle est égale à 0, les deux foyers sont communs avec le centre et l’ellipse devient un cercle. S’il est supérieur ou égal à 1, l’ellipse devient ouverte (parabole ou hyperbole) et d’un point de vue orbital on passe à une trajectoire hyperbolique.
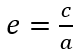
L’excentricité lineaire c dépendant de e et a. on peut donc définir une orbite avec simplement a et e. a définissant la taille et e la forme de l’orbite.
B. Paramètres observables
En dehors de ces données purement géomatiques, la vitesse et le rayon sont des données observables qui permettent de calculer les données géométriques et inversement. Vu qu’on cherche 2 données géomatiques (a et e) on a besoin d’un couple de deux données observables situées au périastre ou à l’apoastre.
Le périastre (périgée dans le système terrestre et périhélie dans le système solaire) est le point de l’orbite le plus proche du corps dominant.
L’apoastre (apogée dans le système terrestre et aphélie dans le système solaire) est le point de l’orbite le plus éloigné du corps dominant.
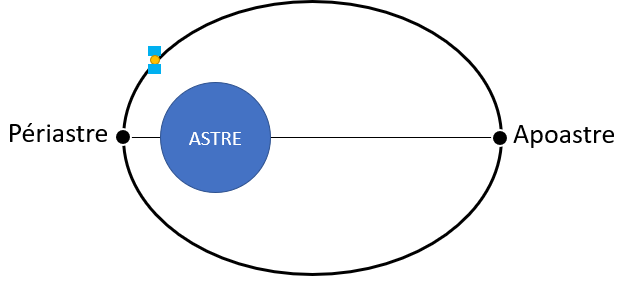
les rayons a ces points sont souvent utilisé pour les calculs et sont noté rayon à l’apoastre ra et le rayon au périastre rp
C. Calculs
couple de données aux extrémités
Le premier couple de données est le couple des extrémités qui nécessite de connaître le ra et le rp. Cela signifie simplement observer le moment où le corps dominé passe au plus près et au plus loin du corps dominant. Vu que le périastre et l’apoastre sont les points les plus éloignés de l’orbite, on peut facilement connaitre a et déduire e de l’écart entre les deux rayons.
Inversement on utilise les relations géomatiques des extrémités de l’orbite et du foyer pour connaitre les rayons à partir des données géomatiques.
formule rayon-vitesse
Si nous connaissons un rayon en un point et la vitesse en ce point (les manœuvres étant souvent faites aux extrémités , on connait la vitesse) nous pouvons aussi calculer les données géométriques. Pour cela nous avons besoin de la relation entre rayon et vitesse en tout point de l’orbite elliptique.
En l’inversant, on peut calculer a en tout point si on connait le rayon et la vitesse en ce point.
couple de données au périastre
Donc on peut utiliser le couple de données au périastre, vitesse et rayon. On utilise la relation rayon<=>vitesse pour calculer a puis on en déduit e.
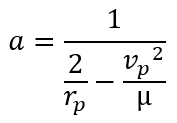
rp: rayon au périastre
vp:vitesse au periastre
mu: paramètre gravitationnel standard
Dans le sens inverse avec les données géométriques, on peut calculer le rayon au périastre avec la vitesse en ce point avec une relation dédiée.
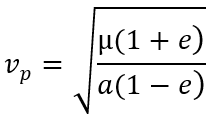
mu: paramètre gravitationnel standard
e : excentricité
a : demi grand axe
Couple de données a l’apoastre
De même, on peut utiliser le couple de données de l’apoastre comprenant aussi le rayon et la vitesse et en adapter les relations pour trouver les données géométriques.
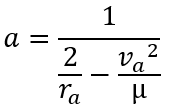
ra: rayon a l’apoastre
va: vitesse a l’apoastre
mu: paramètre gravitationnel standard
Et dans le sens des paramètres géomatiques vers apoastre, nous avons déjà le rayon, et la vitesse est calculée ainsi.
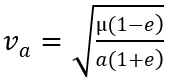
mu: paramètre gravitationnel standard
e : excentricité
a : demi grand axe
D. orbite circulaire
L’orbite circulaire est un cas particulier de l’orbite elliptique, son excentricité est égale a 0. Il n’y a donc ni apoastre ni periastre car tous les points de l’orbite sont à la même distance r (r=a) du corps dominant. On a donc simplement une relation entre le rayon et la vitesse.
C’est grâce à l’orbite circulaire qu’on définit la vitesse orbital minimal. Effet la vitesse minimal pour une mise en orbite autour d’une planète est l’orbite circulaire dont le rayon est juste au-dessus de l’astre ou de son atmosphère s’il en a un.
E. Période
La période, c’est-à-dire le temps que prend le corps à parcourir l’intégralité de son orbite, se calcule grâce aux données géométriques avec la formule ci-dessous et donne un résultat en secondes.
voici ci dessous, une fiche récapitulative des formules pour passé d’un couple de données a l’autre.
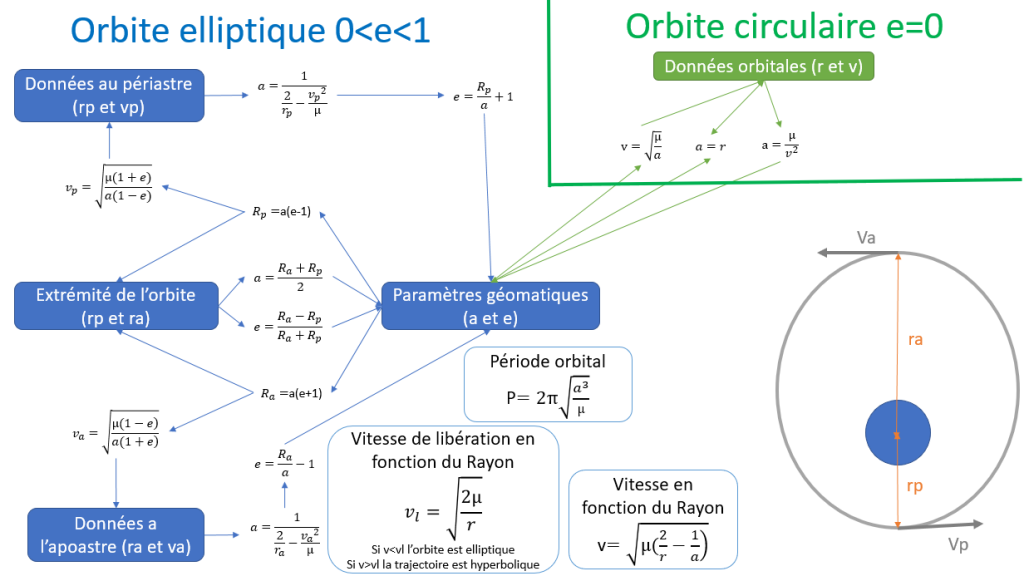
Afin de rendre tout c’est calcul plus concret et de mieux comprendre leur utilité, voici une application numérique