For this digital application, we will calculate the Dv budget of the Venus Express mission (VEX), which has been placed in a very eccentric orbit around Venus. We will simplify by considering that the two planets are on the same orbital plane and that their orbit is circular (Venus and Earth having respectively the 1st and 3rd must circular orbit of the solar system).
Data
The Sun’s standard gravitational parameter: 132 712 440 018 km3 s-2
Venus’ standard gravitational parameter: 324 859 km3 s-2
Earth’s standard gravitational parameter: 398 600 km3 s-2
Venus Radius: Rv= 6,051.8 km
Radius of the Earth: RT=6,378.1 km
semi-major axis of Venus: av=108 208 930 km
semi-major axis of the Earth: at= 149 597 887.5 km
Earth parking orbit:
Circular orbit altitude: H=250km
Venusian orbit targeted:
Apoastre altitude:ha=66 000 km
Calculations
To begin this travel, Vex was put into low Earth orbit by a Soyuz FG rocket from the Baikonur Cosmodrome in Kazakhstan. This launch consists of placing the probe and an upper stage (fregat) in a parking orbit that will be considered circular 250km above sea level. After 1 hour and 36 minutes in this parking orbit, the fregat stage turned on and sent it onto the interplanetary trajectory.
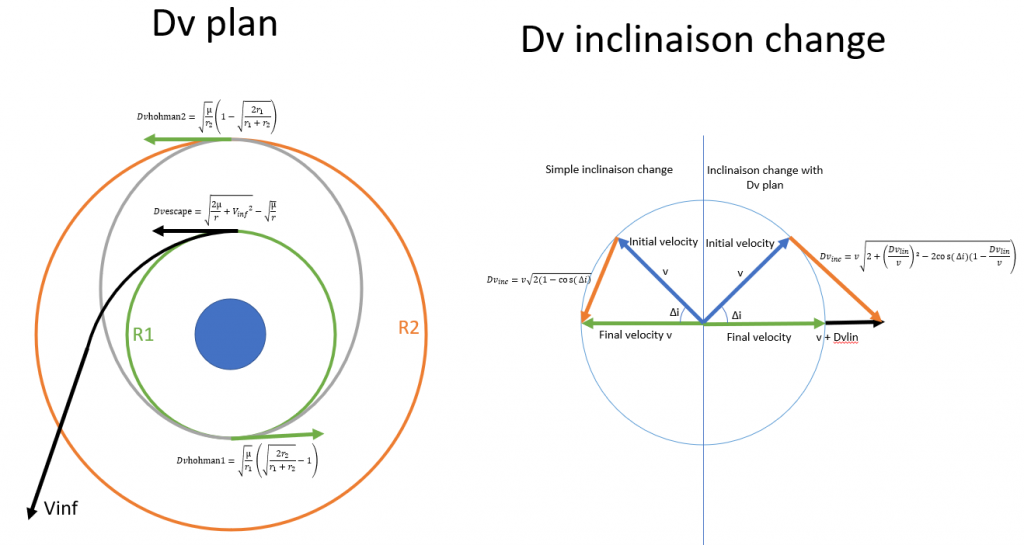
To know the Dv needed to pass on an interplanetary trajectory , it is necessary to define the interplanetary transfer orbit. As we move from one circular orbit to another, we use the most economical transfer orbit that is Hohmann’s orbit in the solar system. So we have perihelion (periastre in the solar system) at the orbit of Venus (rp=av=108 208 930 km) and an aphelia at the Earth’s orbit (ra= at=149 597 887.5 km). It is therefore possible to calculate the velocity which Vex must leave the Earth system to follow this transfer orbit because it corresponds to Dv2 from Hohmann’s orbit.

We can therefore deduce the Dv needed from a circular Earth parking orbit of 250km altitude (thus 6,628.1km radius).
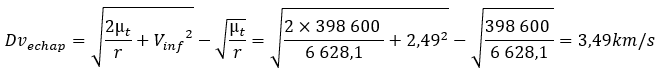
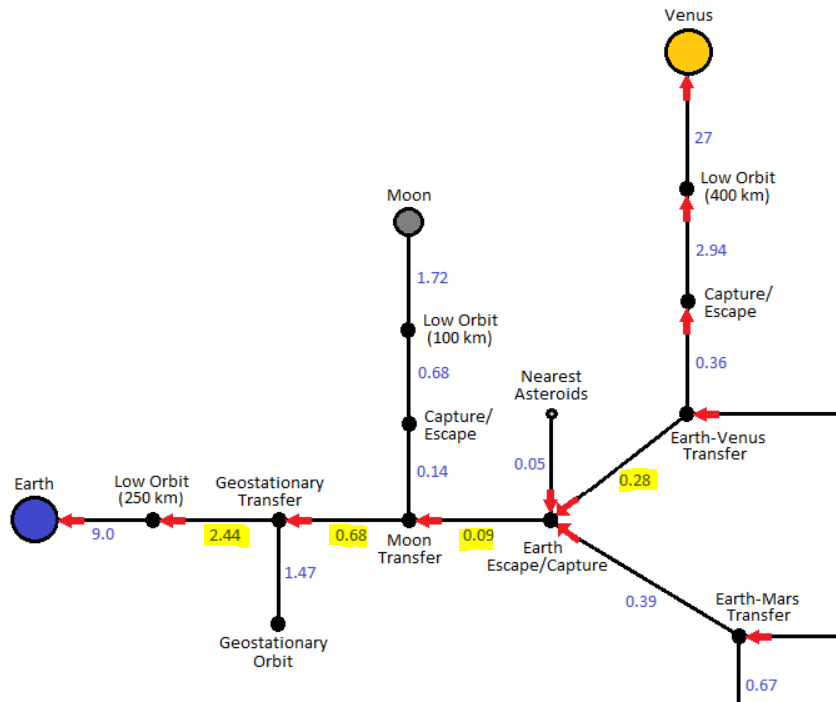
Compared to the Dv map below, the sum of the lines between the low orbit and the earth-venus transfer orbit is equal to 3.49km/s.
Since the Earth is located at the aphelia and Venus in perihelion, Vex had to travel half the orbit before reaching its destination. The duration of the trip is therefore half the period that can be easily calculated after finding the semi main axis has.
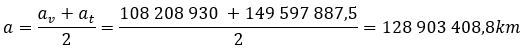

The eccentric orbit aimed around Venus is not usual, so is not found on a map of Dv or ready-to-use formula. The difference in velocity between the initial trajectory and the target orbit must be calculated at one point. A Dv is always more effective as close as possible to the dominant body so the hyperbolic trajectory must have the same periastre as the orbit targeted in order to be able to make the orbital maneuver at this point.
We must therefore start by calculating the velocity at infinity with which Vex enters the Venusian system, it is the Dv1 of Hohman’s transfer orbit.
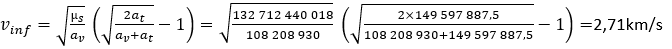
Since we know the velocity at infinity and altitude at the periastre (the same as the intended orbit) we can calculate the velocity at this point on the hyperbolic trajectory.
Rp=Hp+Rv=250+6 051.8=6 301.8km
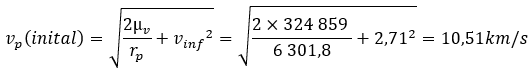
The velocity of the periastre of the target orbit must now be calculated by calculating the geometric data.
ra=ha+Rv=66 000 +6,051.8 = 72 051.8km
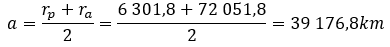
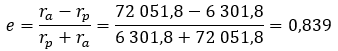

The dv needed to go into orbit is therefore the difference between the initial and final velocity.
Dvcapture=9.73-10.51=0.78km/s
Let’s imagine the inclination of arrival is not that desired for the work orbit and that both are shifted by 10 degrees with the intersection points at the apoastre and the perastre. The most economical is a maneuver at the passage to the apoastre, so you have to start by calculating the velocity at this level before calculating the Dv of the maneuver.

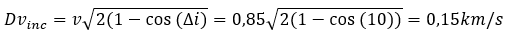
The total dv budget of the mission is therefore the sum of all these Dv, that of exhaust, capture and inclinaison change.
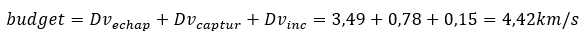
To this budget must be added reserves for the many small maneuvers of correction of trajectory during its 8 years of mission.