A. Généralités
Les déplacements sur Terre et dans l’espace obéissent à des lois physiques radicalement différentes. Sur Terre, tout est soumis aux frottements (de l’air ou des roulements) et conserver un mouvement demande un apport constant d’énergie. On calcule l’autonomie comme étant la distance parcourable avec l’énergie disponible à bord. Dans l’espace, il n’y a pas de frottement, donc un objet ne perd pas d’énergie et une fois en orbite il y reste. A titre d’exemple, le plus ancien satellite encore en orbite, Vanguard 1 lancé en 1958, a parcouru 240 000 orbites soit 9,6 milliards de km survolés alors qu’il est dépourvu de propulsion.
On calcule donc l’autonomie comme étant la capacité à changer d’orbite. Comme vu plus haut, on peut connaitre l’orbite d’un objet en connaissant son rayon et sa vitesse. On peut donc changer d’orbite en un point avec un changement entre la vitesse initial et la vitesse finale de la poussée. On appelle un delta-V, ou ΔV ou encore Dv exprimé en m/s ou km/s le changement de vitesse de la manœuvre.
Le premier Dv à appliquer est celui qui permet de quitter l’atmosphère qui est fournie par le lanceur (nom technique de la fusée). Mais le lancement obéit à des lois très différentes du reste du voyage spatial. Certaines lanceurs déposent leur cargaison (appelée charge utile) sur une orbite parking ou orbite d’attente circulaire d’environ 250km d’altitude avant de continuer son voyage et d’autres continuent directement vers une orbite de transfert. Malgré tout, vu que c’est à partir de cette orbite que les lois de la mécanique spatiale s’appliquent, c’est à partir de là que se calcule le Dv.
B. transfert de Hohmann
Une orbite de transfert est une orbite sur laquelle se place un satellite pour passer d’une orbite initiale à une orbite finale qui n’ont pas de points d’intersection. On peut citer le cas récurant du passage d’une orbite circulaire à une autre (le plus souvent l’orbite géostationnaire). Faute de point d’intersection et vu qu’un satellite repassera toujours par le point où il a effectué sa dernière manœuvre, il n’est pas possible de passer directement d’une orbite à l’autre.
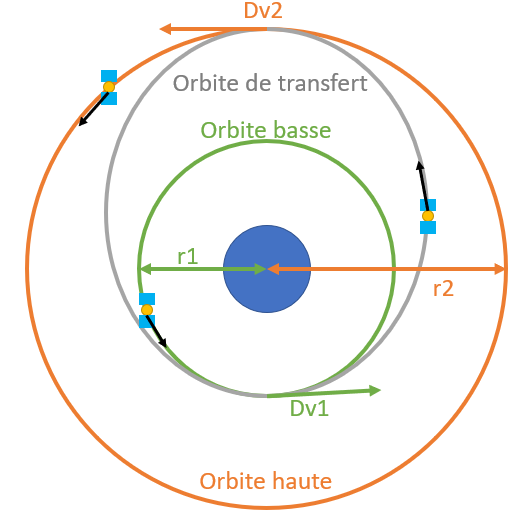
Dans ce cas l’orbite la plus utilisée (car souvent la plus économique) est appelé orbite de transfert de Hohmann. C’est une orbite elliptique où le périgée se situe sur l’orbite circulaire la plus basse (souvent l’l’orbite d’attente) et l’apogée l’orbite circulaire la plus haute comme l’orbite géostationnaire (dans ce cas particulier l’orbite de Hohmann est appelé orbite de transfert géostationnaire ou GTO). Pour passer de l’orbite d’attente à l’orbite géostationnaire, il faut donc deux manœuvres orbitales. La première consiste à augmenter la vitesse de Dv1 en un point de l’orbite qui deviendra le périgée (le point le plus proche de la Terre). L’altitude du reste de l’orbite va croitre et en fin de manœuvre, l’apogée (placée en opposition du périgée) sera au niveau de l’orbite visée. Après avoir effectué une demi-orbite, le satellite arrive à l’apogée et peut faire la deuxième manœuvre qui consiste à augmenter la vitesse de Dv2 afin de faire monter le périgée à la même altitude que l’apogée et donc circulariser l’orbite. Les orbites de Hohmann étant couramment utilisées, on a des équations simplifiées pour calculer Dv1 et Dv2 en fonction des rayons des orbites circulaires basse (r1) et haute (r2).
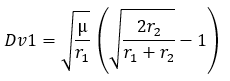
mu: Paramètre gravitationnel standard
r1 et r2: rayons des orbites circulaire basse et haute
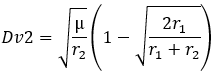
mu: Paramètre gravitationnel standard
r1 et r2: rayons des orbites circulaire basse et haute
C. lancement interplanétaire
Un autre cas souvent rencontré est le départ vers une autre planète. Si on considère, pour simplifier, que l’orbite des planètes est circulaire dans le système solaire, le trajet le plus économique entre deux planètes est donc l’orbite de hohmann entre ces deux orbites, vu que la planète se déplace à la vitesse dictée par son orbite circulaire. Les Dv de Hohman, vu dans la partie précédente, sont donc les vitesses a l’infini d’entrée et de sortie du système planétaire de départ et d’arrivée. Une fois que l’on connait cette vitesse, on peut connaitre la vitesse que la sonde doit avoir aux abords de la Terre pour avoir la vitesse a l’infini souhaitée en s’éloignant de la Terre. On a donc une formule simplifiée du Dv nécessaire à apporter à une sonde sur une orbite d’attente circulaire de rayon r pour atteindre une vitesse a l’infini Vinf.
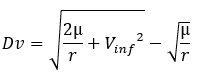
mu: parametre de gravitationnel standard
Vinf: vitesse a l’infini visé
r: rayon de l’orbite de départ
D. changement d’inclinaison
Il est parfois nécessaire de changer l’inclinaison d’une orbite. La manœuvre doit à un des deux points d’intersection du plan orbital initial et final (appelé nœud). Le but de la manœuvre consiste à dévier la composante initiale de vitesse pour qu’elle corresponde à vitesse de l’orbite finale. Si l’on souhaite avoir les mêmes paramètres orbitaux (périastre et apoastre) avant et après, il faut conserver la même vitesse orbitale v, le Dv se calcule avec la formule ci-dessous. Le Dv est fortement dépendant du changement d’inclinaison (Δi) mais aussi de la vitesse orbitale (v) qu’il faut réduire au minimum. Il faut donc privilégier une manœuvre à l’apoastre. Ce facteur est tel que pour les gros changements d’inclinaison, comme par exemple les satellites géostationnaires (inclinaison de 0°) tirés depuis des latitudes élevées (Baïkonour 45°) sont envoyés sur une orbite surpersynchrone. Ces orbites ont un apogée plus élevé que l’orbite géostationnaire afin d’y avoir une vitesse plus faible et ainsi diminuer le Dv de la manœuvre.
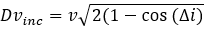
v: vitesse au moment de la manœuvre
Di: différence d’inclinaison souhaité
Si, en plus du changement d’inclinaison, il est nécessaire d’effectuer dans le plan (comme un Dv de hohmann), il est possible de fusionner les deux manœuvres car le Dv combiné et moins élevé que la somme des deux manœuvres séparées. C’est notamment le cas d’un lancement d’un satellite géostationnaire depuis Kourou qui peut simultanément appliquer son Dv de circularisation (deuxième Dv de hohmann) tout en rattrapant un décalage d’inclinaison de 5° dû à la latitude de la Guyane. On utilise la relation ci-dessous avec Dvlin le delta-V de la manœuvre dans le plan.
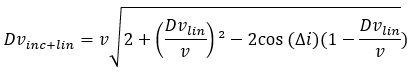
v: vitesse au moment de la manœuvre
Dvlin: Dv dans le plan souhaité
Di: différence d’inclinaison souhaité
Vous trouverez ci-dessous une fiche récapitulative des formules de Dv les plus usuels.
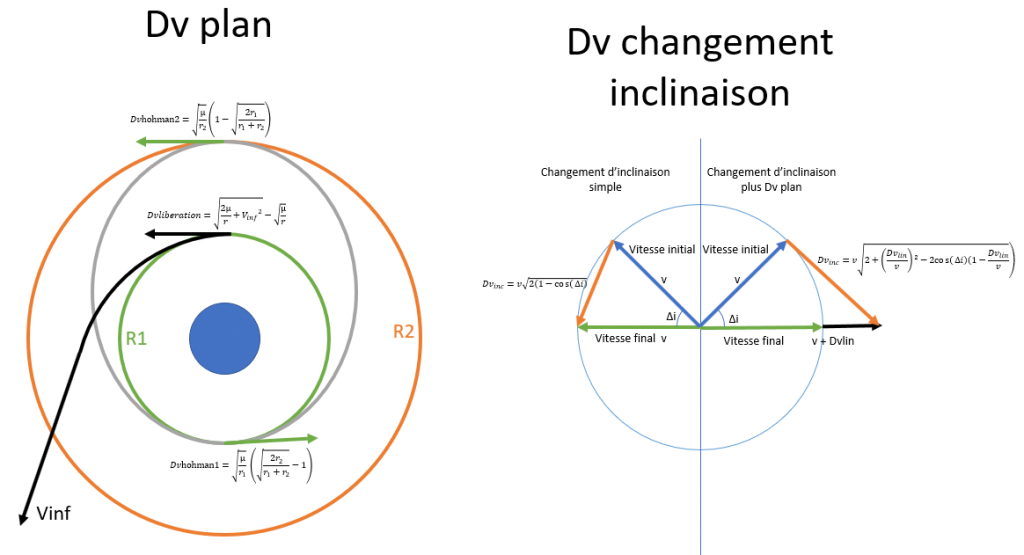
E. budget Dv
Le budget Dv est défini par la somme des Dv qui devront être accomplies au cours de l’ensemble d’une mission. Il doit être inférieur à la capacité du vaisseau et de son lanceur à lui fournir de la vitesse.
Pour éviter d’avoir à faire les calculs décrits ci-dessous, on peut trouver une estimation des Dv courants sur une Carte de Dv. Chaque trait représente une manœuvre entre deux orbites, avec pour chaque le Dv associé. Pour avoir une estimation du budget Dv d’une mission, il suffit de faire la somme de tous les traits entre le point de départ et d’arrivée de la mission. Attention, la majorité des cartes de Dv (delta-V map en anglais), disponibles sur internet concerne le jeux vidéo KSP qui sont faciles à reconnaitre car les planètes n’ont pas leur vrai nom ni leur vrai cortège de satellites.
Vous trouverez ci-dessous un lien vers une des cartes de Dv les plus complètes disponible pour le système solaire.
Afin de rendre tout c’est calcul plus concret et de mieux comprendre leur utilité, voici une application numérique