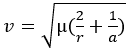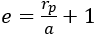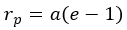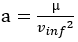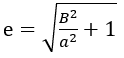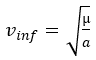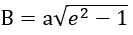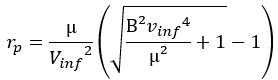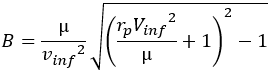A. données géométrique
L’hyperbole est une conique plan ouvert. Elle est définie par les mêmes paramètres géométriques que ellipse mais qui ont encore moins de réalité physique.
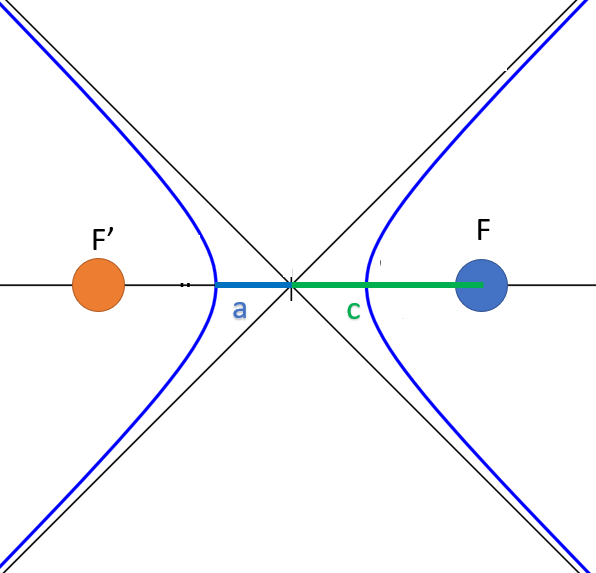
Les foyers F et F’ dont un (le point F) est la position du corps dominant. le foyer F’ n’a aucun réalité physique. En effet , l’hyperbole géomatique se défini par deux courbes symétriques situer autour de chaque foyer. Physiquement, la trajectoire hyperbolique n’est qu’une seul de ces courbes, celle ayant le corps dominant comme foyer.
Le grand axe 2a est le plus petit segment entre deux points de l’hyperbole.La valeur a qui caractérise le demi-grand axe est souvent utilisée.
L’excentricité linéaire c qui est égale à la moitié de la distance FF’.
L’excentricité e est un paramètre sans dimension qui décrit la forme globale de l’hyperbole. Si elle est inférieur a 1, c’est une ellipse et d’un point de vue orbital on est sur une orbite elliptique. Pour une trajectoire hyperbolique , elle est supérieur a 1.
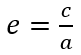
L’excentricité linéaire c dépendant de e et a. on peut donc définir une trajectoire avec simplement a et e. a définissant la taille et e la forme de l’orbite.
B. Paramètres observable
Les données géométriques n’ayant pas de réalité physique, il est nécessaire d’introduire des paramètres observable. Pour cela il faut des couples de données en deux points.
Comme pour l’orbite elliptique on a le périastre (périgée dans le système terrestre et périhélie dans le système solaire) est le point de l’orbite le plus proche du corps dominant. le couple de donnée en ce point est le rayon au périastre rp et la vitesse au périastre vp
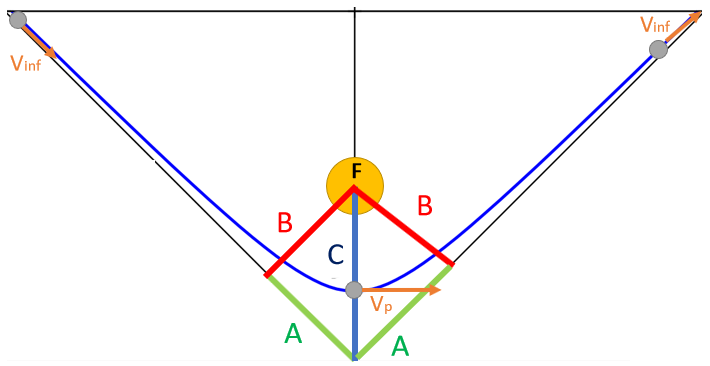
L’hyperbole étant ouvert, il n’y a pas d’apoastre . Par contre, dans un cas comme un astéroïde approchant de la Terre il faut calculer les risques de collision (notamment le rayon au périastre) avant d’arrivé au périastre (et donc à la collision). On utilise donc les données a l’entrée du système dites a l’infini car elles sont calculées pour des distance très éloignée du corps dominant. on défini donc la vitesse à l’infini Vinf ou V∞ qui est la vitesse que possède le corps dominé en entrant dans le système du corps dominé. Le deuxième est l’écart B entre l’asymptote et le foyer. L’asymptote est l’axe que suit l’objet avant de rentrer dans le système et avant d’être perturbé par le corps dominant. L’écart B est donc la distance minimale entre les corps dominant et dominé si le corps dominant n’avait pas d’influence gravitationnelle.
Calcul
relation rayon-vitesse
Sur une trajectoire hyperbolique la relation vitesse-rayon existe toujours mais est modifiée.
Couple de données au périastre
On peut aller des données au périastre vers les données géométriques on commence par inverser la relation rayon-vitesse pour connaitre a puis on en déduit e.
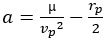
mu: paramètre gravitationnel standard
vp: vitesse au périastre
rp: rayon au périastre
On peut aussi faire le calcul du sens des données géométriques vers données au périastre en calculant a: demi grand axe puis en utilisant la relation rayon-vitesse appliquée au périastre.
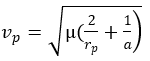
mu: paramètre gravitationnel standard
rp: rayon au périastre
a: demi grand axe
Couple de donnée a l’infini
On a un couple de données dit à « l’infini » Vinf et B avec des paramètres observables au moment de la rentrée dans le système. On peut même anticiper bien plus, par exemple, en connaissant les paramètres orbitaux d’un astéroïde autour du soleil, on peut connaitre les paramètres au passage près de la Terre des décennies à l’avance. On peut donc calculer le demi-grand axe directement avec la vitesse infini puis en déduire l’excentricité avec les relations géométriques.
On peut aussi utiliser des relations directes permettant de calculer les données à l’infini avec les paramètres géométriques.
calcul direct périastre-infini
Grâce à des relations plus complexes, on peut calculer les données au périastre directement avec celles à l’infini, ainsi on peut juger de la dangerosité d’un astéroïde, car si le rayon au périastre est inférieur au rayon de la planète, il y a impact et l’énergie de cet impact dépend de la vitesse au périastre.
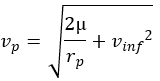
mu: paramètre gravitationnel standard
rp: rayon au périastre
vinf: vitesse infini
On peut aussi faire le calcul inverse afin de connaitre les conditions de sortie du système à partir de la vitesse donnée à une sonde interplanétaire depuis une orbite parking
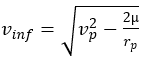
vp: vitesse au périastre
mu: paramètre gravitationnel standard
rp: rayon au périastre
voici ci-dessous, une fiche récapitulative des formules pour passer d’un couple de données a l’autre.
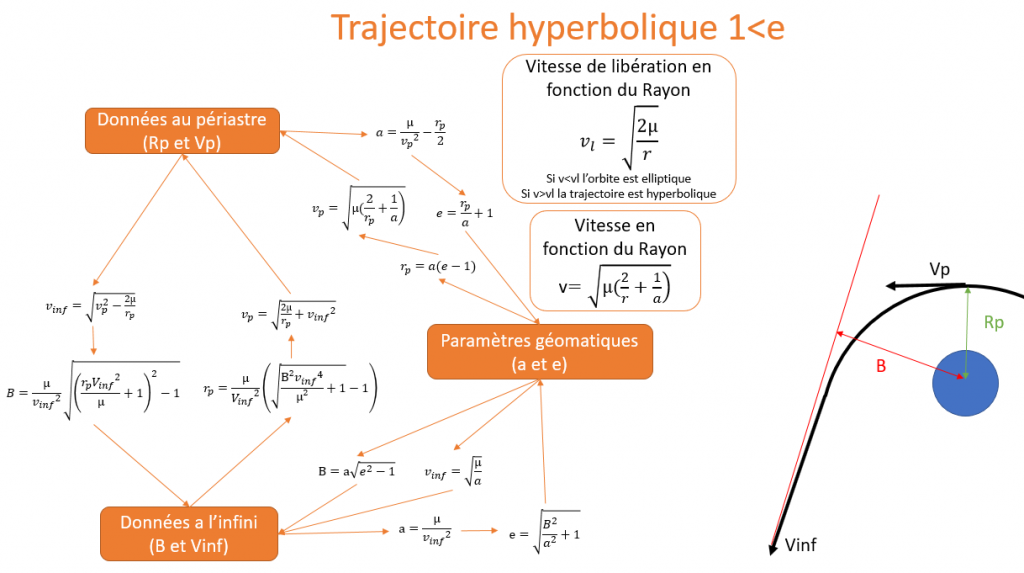
Afin de rendre tout c’est calculs plus concret et de mieux comprendre leurs utilités, voici une application numérique