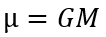Gravitation
La mécanique orbitale décrit le mouvement des corps massique dans le vide et soumis uniquement aux lois de la gravitation.
La gravitation est une interaction fondamentale qui crée une force d’attraction entre deux objets possédant une masse. La valeur de cette force est donnée par la formule :
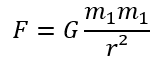
F : la force gravitationnelle exerce par les deux corps exprimée en N
G : la constante gravitationnelle toujours égale à 6,6742×10-11 N·m2·kg−2
m1 et m2 : les masses des deux objets entre lesquelles se crée l’interaction exprimée en kg
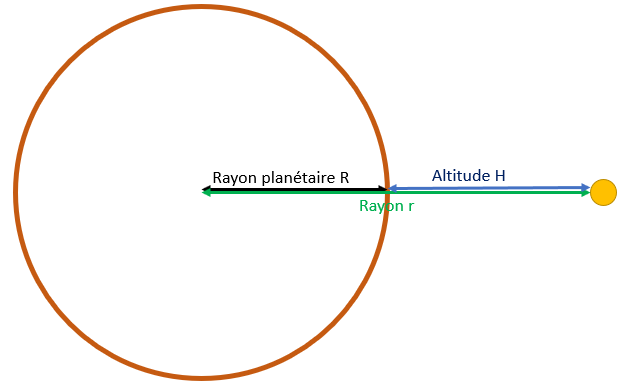
R : Rayon, c’est a dire la distance entre les centre de gravité, exprimé en mètredistance en orbite
Le thème rayon r désigne simplement la distance entre le centre de gravité des deux corps. Il diffère de l’altitude h qui sépare le satellite de la surface d’un astre. Pour passer de l’un à l’autre, il faut ajouter le rayon de l’astre R ou plus souvent Rx (avec x la premier lettre du nom de l’astre pour évité les confusion),c’est-à-dire la distance entre le centre de gravité et la surface.
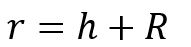
Cette force est réciproque, c’est-à-dire attire les deux objets l’un vers l’autre avec la même force. Donc, la Terre vous attire avec autant de force que vous l’attirez. La masse de la terre étant largement supérieure à la vôtre, la force que vous lui appliquez à un effet négligeable sur son comportement.
Cependant l’attraction gravitationnelle de la Terre sur vous est la principale force qui gouverne vos mouvements. Cette prépondérance est telle, que l’attraction qu’exerce d’autre objet proche (véhicule, bâtiment, personne) de vous est négligeable comparée à la force de la Terre.
Notion de système
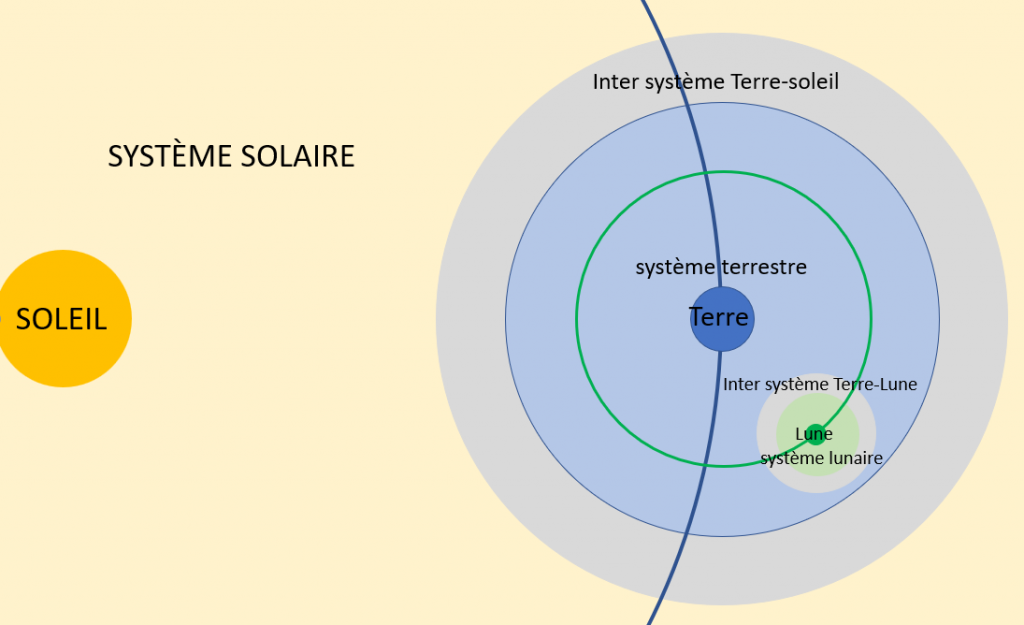
Cette prépondérance d’un objet sur les autres permet de crée une notion de système. Un système est un volume restreint autour d’un objet massif (objet dominant) ou chaque point se trouve beaucoup plus près de l’objet dominant que de tout autre objet de masse équivalant ou supérieure. Les autres objets du système (objet dominé) ont donc une masse largement plus faible. La force de dominant sur le dominé est la seule prise en compte. Les forces du dominé sur les dominants, des dominés entre eux et des objets extérieurs au système sur les dominés est négligée.
Des systèmes peuvent être imbriqués l’un dans l’autre. Par exemple, le système solaire a pour objet dominant le soleil et comme objets dominés, les planètes, mais chaque planète a son propre système. Dans le système terrestre (ou la Terre est l’objet dominant) la trajectoire des satellites est gouvernée par la Terre, et non le soleil, plus massif mais plus éloigné (la force d’attraction dépend du carré de la distance).
La notion de système est imparfaite car, en se rapprochant des frontières d’un système, les objets dominés (comme des satellites terrestres) sont de plus en plus perturbés par des objets dominants de systèmes supérieurs (soleil) ou inférieurs (lune), au point que des corrections permanentes sont nécessaires. On peut même placer un objet entre deux systèmes et avoir une trajectoire gouvernée par les deux corps dominants (exemple orbite NRHO).
Pour simplifier les calculs à l’intérieur d’un système, on introduit le paramètre gravitationnel standard µ du corps dominant qui se calcule simplement par :
Avec G la constante gravitationnelle définie plus haut et M la masse du corps dominant. Dans le système d’unité international (métrique) il est exprimé en m3 s-2, mais pour des raisons pratiques, en mécanique orbitale c’est souvent le km qui est utilisé pour les distances. µ est donc souvent exprimée en km3 s-2 moyennant un facteur 10-9 sur la valeur en m3 s-2
trajectoire et vitesse de transition
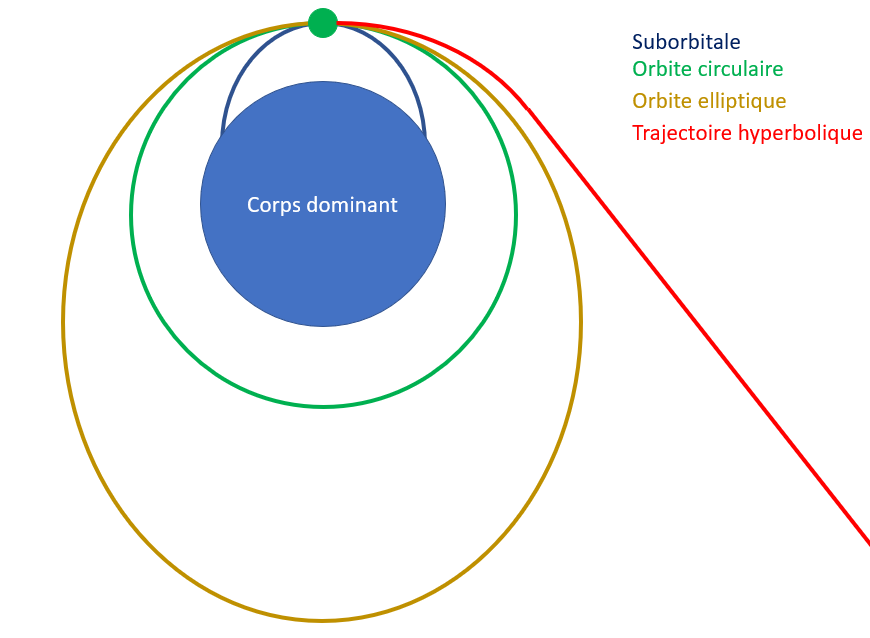
Un corps dominé qui se déplace dans un système possède une énergie qui, faute de frottements, ne varie pas. Cette énergie est répartie entre énergie cinétique qui dépend de la vitesse et l’énergie potentielle qui dépend du rayon. Un corps dominé convertit une partie de sa vitesse en distance ou de distance en vitesse. Selon le niveau d’énergie, il peut suivre 4 types de trajectoire.
- Suborbitale : v<v1 : Si la vitesse est trop faible, l’effet centrifuge n’est pas suffisant pour compenser la gravité. Le corps descend pour reprendre de la vitesse. S’il redescend trop, le rayon devient inférieur au rayon de la planète rendant impossible le maintien dans l’espace. L’objet ne parvenant pas à faire une orbite complète, cette trajectoire est dite suborbitale.
- Orbite circulaire : v=v1 : si le corps a juste assez de vitesse pour que l’effet centrifuge compense la gravité. Le corps reste toujours à la même vitesse et à la même altitude. Il effectue des cercles autour du corps dominant d’où le nom d’orbite circulaire.
- Orbite elliptique : v1<v<v2 : si la vitesse est assez importante pour que l’effet centrifuge surpasse l’attraction gravitationnelle. Le dominé s’éloigne donc du dominant convertissant sa vitesse en rayon. Au bout d’un moment, la vitesse a trop diminué pour compenser la gravité et il descend faisant croître sa vitesse. Le dominé finit par repasser par le point initial, à la même vitesse et donc remonte dans un cycle de montée descente perpétuel. Il suit un circuit en forme d’ellipse qui lui donne son nom d’orbite elliptique.
- Trajectoire hyperbolique : v2<v : si la vitesse est vraiment trop importante, le corps s’éloigne au point que la force de gravitation devient faible. La vitesse diminue de moins en moins alors que le corps continue de s’éloigner. Finalement il s’éloigne à tout jamais et ne revient pas vers le corps dominant.
Pour déterminer dans quel cas on se trouve, il faut calculer les vitesses de transition :
La vitesse d’orbitation v1 est la vitesse nécessaire à atteindre une orbite circulaire.
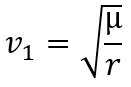
La vitesse de libération v2 est la vitesse de passage d’une orbite elliptique à une trajectoire elliptique.
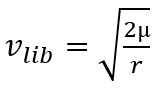
Paramètre non énergétique
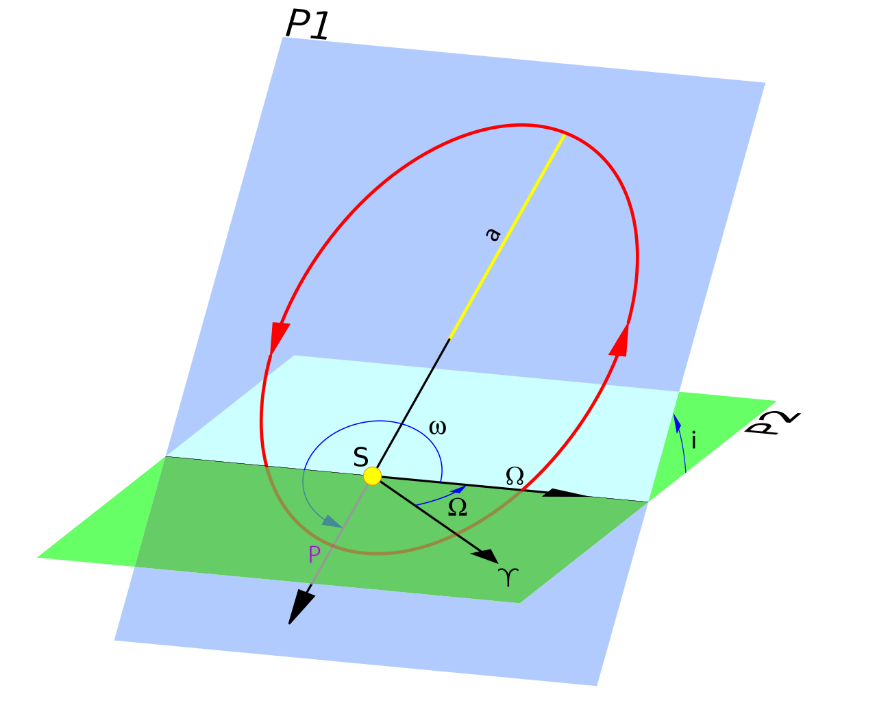
A l’exception de cas particuliers, comme les orbites autour des points de Lagrange (exemple de l’orbite NHRO) toutes les orbites sont planes. On définit l’inclinaison orbitale i comme l’angle séparant le plan orbital et un plan de référence, qui est l’équateur pour un système planétaire ou l’écliptique (plan orbital de la Terre) pour le système solaire. Si on prend l’exemple de la Terre, l’inclinaison est à 0 quand le satellite est en orbite autour de l’équateur dans le sens prograde, c’est-à-dire de l’ouest vers l’est, ou dans le sens direct (inverse des aiguilles d’une montre) vu depuis le pole nord. A 90° d’inclinaison l’orbite passe au-dessus des pôles. A 180° l’orbite est équatoriale mais rétrograde (inverse de prograde).
Le dernier élément à connaitre est l’argument du périastre ω qui définit l’angle sur l’équateur entre le point de référence (appelé point vernal) et la projection sur l’équateur du periastre.